Hypoponera emeryi

Hypoponera emeryi
Scientific classification
Kingdom:	Animalia
Phylum:	Arthropoda
Class:	Insecta
Order:	Hymenoptera
Family:	Formicidae
Subfamily:	Ponerinae
Tribe:	Ponerini
Genus:	Hypoponera
Species:	H. emeryi
Binomial name
Hypoponera emeryi (Donisthorpe, 1943)

Distribution

Distribution based on Regional Taxon Lists

Indo-Australian Region: New Guinea (type locality).

Distribution based on AntMaps

Distribution based on AntWeb specimens

Check data from AntWeb

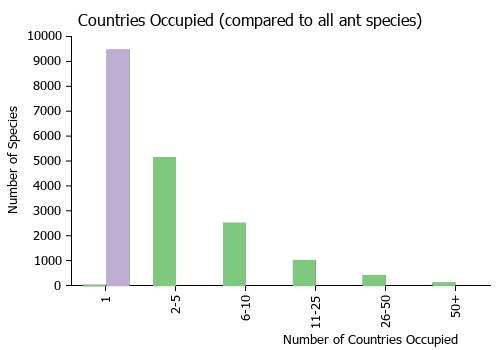
Countries Occupied

Number of countries occupied by this species based on AntWiki Regional Taxon Lists. In general, fewer countries occupied indicates a narrower range, while more countries indicates a more widespread species.

Estimated Abundance

Relative abundance based on number of AntMaps records per species (this species within the purple bar). Fewer records (to the left) indicates a less abundant/encountered species while more records (to the right) indicates more abundant/encountered species.

Nomenclature

The following information is derived from Barry Bolton's Online Catalogue of the Ants of the World.

• emeryi. Ponera emergi Donisthorpe, 1943d: 443 (m.) NEW GUINEA. Justified emendation of spelling to emeryi: Wilson, 1958d: 328. Combination in Hypoponera: Bolton, 1995b: 214.

References

• Bolton, B. 1995b. A new general catalogue of the ants of the world. Cambridge, Mass.: Harvard University Press, 504 pp. (page 214, Combination in Hypoponera)
• Donisthorpe, H. 1943e. The ants (Hym., Formicidae) of Waigeu Island, North Dutch New Guinea. Ann. Mag. Nat. Hist. 11(10): 433-475.(page 443, male described)
• Wilson, E. O. 1958g. Studies on the ant fauna of Melanesia III. Rhytidoponera in western Melanesia and the Moluccas. IV. The tribe Ponerini. Bulletin of the Museum of Comparative Zoology 119: 303-371 (page 328, Justified emendation of spelling to emeryi)

References based on Global Ant Biodiversity Informatics

• Donisthorpe, Horace. 1943. The Ants of Waigeu Island, North Dutch New Guinea. The Annals and Magazine of Natural History 11 (10): 433-475.
• Janda M., G. D. Alpert, M. L. Borowiec, E. P. Economo, P. Klimes, E. Sarnat, and S. O. Shattuck. 2011. Cheklist of ants described and recorded from New Guinea and associated islands. Available on http://www.newguineants.org/. Accessed on 24th Feb. 2011.
• Wilson E. O. 1958. Studies on the ant fauna of Melanesia III. Rhytidoponera in western Melanesia and the Moluccas. IV. The tribe Ponerini. Bulletin of the Museum of Comparative Zoology 119: 303-371.